- paraboloïde
-
paraboloïde [ parabɔlɔid ] n. m.• 1691; adj. 1660 ; de 2. parabole♦ Géom. Quadrique n'ayant pas de centre. Paraboloïde elliptique, hyperbolique, dont certaines sections planes sont des ellipses, des hyperboles. Paraboloïde de révolution : surface engendrée par une parabole tournant autour de son axe de symétrie.
● paraboloïde nom masculin Paraboloïde elliptique, quadrique d'équation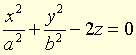 .
Paraboloïde hyperbolique, quadrique d'équation
.
Paraboloïde hyperbolique, quadrique d'équation 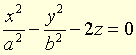 .
Paraboloïde de révolution, paraboloïde elliptique particulier, obtenu quand a = b.
● paraboloïde (expressions)
nom masculin
Paraboloïde elliptique, quadrique d'équation
.
Paraboloïde de révolution, paraboloïde elliptique particulier, obtenu quand a = b.
● paraboloïde (expressions)
nom masculin
Paraboloïde elliptique, quadrique d'équation 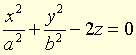 .
Paraboloïde hyperbolique, quadrique d'équation
.
Paraboloïde hyperbolique, quadrique d'équation 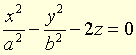 .
Paraboloïde de révolution, paraboloïde elliptique particulier, obtenu quand a = b.
paraboloïden. m. GEOM Surface du second degré dont le centre est rejeté à l'infini et qui admet une infinité de plans diamétraux, tous parallèles à une même droite. Paraboloïde de révolution. Paraboloïde elliptique. Paraboloïde hyperbolique.⇒PARABOLOÏDE, subst. masc.GÉOM. ,,Surface du second degré (quadrique) engendrée par la translation d'une parabole P1 dont le sommet décrit une autre parabole , P2 située dans un plan perpendiculaire au plan de P1, les axes des deux courbes étant supposés parallèles à la direction
.
Paraboloïde de révolution, paraboloïde elliptique particulier, obtenu quand a = b.
paraboloïden. m. GEOM Surface du second degré dont le centre est rejeté à l'infini et qui admet une infinité de plans diamétraux, tous parallèles à une même droite. Paraboloïde de révolution. Paraboloïde elliptique. Paraboloïde hyperbolique.⇒PARABOLOÏDE, subst. masc.GÉOM. ,,Surface du second degré (quadrique) engendrée par la translation d'une parabole P1 dont le sommet décrit une autre parabole , P2 située dans un plan perpendiculaire au plan de P1, les axes des deux courbes étant supposés parallèles à la direction de l'intersection de leurs plans`` (UV.-CHAPMAN 1956). Le paraboloïde peut être elliptique ou hyperbolique (Lar. encyclop.).Paraboloïde elliptique. Surface du second degré dont les axes des deux courbes sont de même sens et dont la surface obtenue, convexe, est coupée suivant une ellipse par tout plan non parallèle à
de l'intersection de leurs plans`` (UV.-CHAPMAN 1956). Le paraboloïde peut être elliptique ou hyperbolique (Lar. encyclop.).Paraboloïde elliptique. Surface du second degré dont les axes des deux courbes sont de même sens et dont la surface obtenue, convexe, est coupée suivant une ellipse par tout plan non parallèle à (d'apr. UV.-CHAPMAN 1956). L'ellipsoïde de rotation donne l'ellipsoïde de forme générale et le paraboloïde de rotation le paraboloïde (elliptique) général (JOEDICKE, Structures en voiles et coques, 1962, p.24).Paraboloïde hyperbolique. Surface du second degré dont les axes des deux courbes sont de sens contraire et dont la surface obtenue, non convexe, est coupée suivant une hyperbole par tout plan non parallèle à
(d'apr. UV.-CHAPMAN 1956). L'ellipsoïde de rotation donne l'ellipsoïde de forme générale et le paraboloïde de rotation le paraboloïde (elliptique) général (JOEDICKE, Structures en voiles et coques, 1962, p.24).Paraboloïde hyperbolique. Surface du second degré dont les axes des deux courbes sont de sens contraire et dont la surface obtenue, non convexe, est coupée suivant une hyperbole par tout plan non parallèle à (d'apr. UV.-CHAPMAN 1956). Le paraboloïde hyperbolique était pour lui [Antonio Gaudi] le symbole de la sainte Trinité. Deux droites, les directrices, toutes deux identiques et infinies, symbolisaient pour lui le Père et le Fils. Dans la troisième droite, la génératrice qui se déplace sur les deux directrices pour engendrer la surface, Gaudi voyait le signe du Saint Esprit, car la génératrice réunit les deux directrices et est de même nature (JOEDICKE, Structures en voiles et coques, 1962 p.11).♦En appos. avec valeur d'adj. La forme du vaisseau en coque paraboloïde (MAIZIÈRE, Nouv. archit. nav., 1853, p.2).— En partic. Paraboloïde de révolution. ,,Surface obtenue en faisant tourner une parabole autour de son axe de symétrie; cas particulier du paraboloïde elliptique`` (UV.-CHAPMAN 1956). Les problèmes relatifs à la spirale n'ont «rien de commun» avec certains autres relatifs à la sphère et au paraboloïde de révolution (BOURBAKI, Hist. math., 1960, p.180).♦OPT. ,,Surface réfléchissante donnant en son foyer une image parfaite d'un point situé à l'infini sur son axe`` (Lar. Lang. fr.). Au lieu de donner au miroir la forme d'un paraboloïde de révolution et de placer la source au foyer, on lui donne la forme d'un cylindre parabolique et on place l'excitateur suivant la ligne focale (H. POINCARÉ, Théorie Maxwell, 1899, p.55). Dans le cas des miroirs (...). Si la surface est un paraboloïde de révolution, les points conjugués stigmatiques sont le foyer F et le point à l'infini dans la direction de l'axe (PRAT, Opt., 1962, p.141).Prononc. et Orth.:[
(d'apr. UV.-CHAPMAN 1956). Le paraboloïde hyperbolique était pour lui [Antonio Gaudi] le symbole de la sainte Trinité. Deux droites, les directrices, toutes deux identiques et infinies, symbolisaient pour lui le Père et le Fils. Dans la troisième droite, la génératrice qui se déplace sur les deux directrices pour engendrer la surface, Gaudi voyait le signe du Saint Esprit, car la génératrice réunit les deux directrices et est de même nature (JOEDICKE, Structures en voiles et coques, 1962 p.11).♦En appos. avec valeur d'adj. La forme du vaisseau en coque paraboloïde (MAIZIÈRE, Nouv. archit. nav., 1853, p.2).— En partic. Paraboloïde de révolution. ,,Surface obtenue en faisant tourner une parabole autour de son axe de symétrie; cas particulier du paraboloïde elliptique`` (UV.-CHAPMAN 1956). Les problèmes relatifs à la spirale n'ont «rien de commun» avec certains autres relatifs à la sphère et au paraboloïde de révolution (BOURBAKI, Hist. math., 1960, p.180).♦OPT. ,,Surface réfléchissante donnant en son foyer une image parfaite d'un point situé à l'infini sur son axe`` (Lar. Lang. fr.). Au lieu de donner au miroir la forme d'un paraboloïde de révolution et de placer la source au foyer, on lui donne la forme d'un cylindre parabolique et on place l'excitateur suivant la ligne focale (H. POINCARÉ, Théorie Maxwell, 1899, p.55). Dans le cas des miroirs (...). Si la surface est un paraboloïde de révolution, les points conjugués stigmatiques sont le foyer F et le point à l'infini dans la direction de l'axe (PRAT, Opt., 1962, p.141).Prononc. et Orth.:[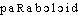 ]. Att. ds Ac. 1935. Étymol. et Hist.1. 1660 adj. «produit par la circonvolution entière d'une parabole autour de son axe`` (HUYGENS, OEuvres complètes, éd. Sté hollandaise des sc., La Haye, t.3, 1890, p.27: lignes paraboloides); 2. 1691 subst. masc. «solide produit par la circonvolution entière d'une parabole autour de son axe» (OZANAM d'apr. FEW t.7, p.614a); 1808 subst. fém. (BOISTE); 3. 1868 masc. «surface du second degré ne possédant pas de centre, mais seulement un axe de symétrie» (LITTRÉ). Dér. de parabole2; suff. -ide2. Bbg. QUEM. DDL t.22.paraboloïde [paʀabɔlɔid] n. m.ÉTYM. 1691; attesté comme adj. en 1660; de 2. parabole, et suff. -oïde.❖♦ Géom. Surface du second degré qui est engendrée par une parabole se déplaçant de manière telle que son plan reste constamment parallèle à lui-même et que son sommet décrive une autre parabole fixe dont le plan est perpendiculaire au plan de la parabole mobile; quadrige n'ayant pas de centre. || Paraboloïdes elliptiques, hyperboliques, dont certaines sections planes sont des ellipses, des hyperboles. || Paraboloïde de révolution.❖DÉR. Paraboloïdal.
]. Att. ds Ac. 1935. Étymol. et Hist.1. 1660 adj. «produit par la circonvolution entière d'une parabole autour de son axe`` (HUYGENS, OEuvres complètes, éd. Sté hollandaise des sc., La Haye, t.3, 1890, p.27: lignes paraboloides); 2. 1691 subst. masc. «solide produit par la circonvolution entière d'une parabole autour de son axe» (OZANAM d'apr. FEW t.7, p.614a); 1808 subst. fém. (BOISTE); 3. 1868 masc. «surface du second degré ne possédant pas de centre, mais seulement un axe de symétrie» (LITTRÉ). Dér. de parabole2; suff. -ide2. Bbg. QUEM. DDL t.22.paraboloïde [paʀabɔlɔid] n. m.ÉTYM. 1691; attesté comme adj. en 1660; de 2. parabole, et suff. -oïde.❖♦ Géom. Surface du second degré qui est engendrée par une parabole se déplaçant de manière telle que son plan reste constamment parallèle à lui-même et que son sommet décrive une autre parabole fixe dont le plan est perpendiculaire au plan de la parabole mobile; quadrige n'ayant pas de centre. || Paraboloïdes elliptiques, hyperboliques, dont certaines sections planes sont des ellipses, des hyperboles. || Paraboloïde de révolution.❖DÉR. Paraboloïdal.
Encyclopédie Universelle. 2012.
